Hannah Schwartz (Mathematics) has accepted two prestigious postdoctoral positions with the Max Planck Institute for Mathematics in Bonn, Germany and with the Department of Mathematics at Princeton University, beginning Fall 2019 and 2020, respectively. Before moving to Germany this Fall, Hannah will be presenting her work at conferences in France and Canada. She will also spend a week researching with collaborators at the American Institute of Mathematics.
These successes come off the heels of recently defending her Ph.D. dissertation “Exotic Phenomena in Dimension Four”.
Hannah’s research focuses on a branch of mathematics called “topology”, in which one studies the intrinsic and global qualities of different spaces. For instance, unlike geometry in which shapes must stay rigid, spaces in topology can be manipulated as long as the general properties of the space are not lost. A classic example is the equivalence (at least to topologists) of a coffee cup and a donut, since these shapes can be stretched and morphed to resemble one another.
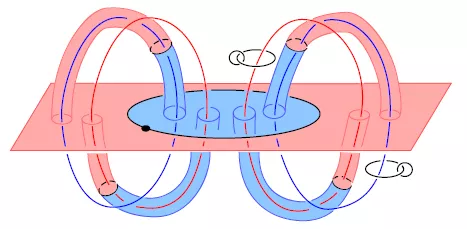
Hannah’s work looks at nice spaces, called manifolds. Like spatial dimensions often considered in physics, manifolds are increasingly complicated when more dimensions are introduced. Part of Hannah’s dissertation - and ongoing research - is an effort to visually represent and envisage four dimensional manifolds. Hannah has sought out new ways to relate topologically similar manifolds to each other through her research.
The next part of Hannah’s dissertation looks more directly at a single four manifold, rather than comparing the behavior of many. Hannah is interested in the way that spheres (much in the sense of spheres that we are familiar with in 3D) appear and behave within a single four manifold. She explains “as an analogy if you squint your eyes while looking at a square and a circle, they might appear to be the same. Yet, as you open your eyes, they become clearer and their differences are more apparent. Likewise, if I look at two different spheres within a single four manifold – they might look the same if I squint my eyes and different when I am more in focus. Maybe I will find that it is not possible to, say, move one sphere into the other.” It is this line of research that she sees herself continuing post-Bryn Mawr.